かつての受験生が合否を知る手段だった「サクラサク」の電報。合格か不合格か、たった1ビットの情報に過ぎないはずの結果が、実は約21ビットという恐ろしく非効率な方法で伝達されていたとしたら?
これは、情報理論の父、クロード・シャノンが提唱した「通信速度の究極の限界」に真っ向から逆らう、「シャノン先生ブチギレ符号化」です。
本エピソードでは、情報理論の基本概念であるエントロピーと情報源符号化定理を用いて、「サクラサク」の非効率性を徹底解剖します。そして、現代のデータ圧縮やAI通信にも通じる、モールス信号が実現した効率の極致までを深掘りします。
📚 受験結果のエントロピーは1ビット!「サクラサク」が極端な電報 非効率だった理由
コンピュータ科学の土台の一つである情報理論は、情報そのものが持つ不確かさや価値を定量的に扱う学問です。その核となる概念がエントロピーです。
合否の不確かさは、たったの1ビット
情報理論において、ある情報源が持つ「不確かさの度合い」はエントロピーという値で表現されます。これは、その情報を伝達するために理論上最低限必要な情報量を示します。
数学的には、情報源のエントロピー ( H(X) ) は、シャノンの式で表されます。
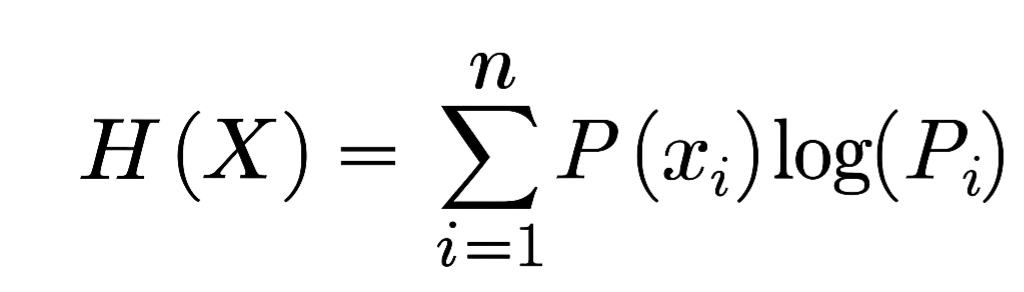
例えば、受験結果は「受かるか落ちるか」という二つの事象しかありません。それぞれの確率が「2分の1ずつ」だと仮定した場合、この情報源(受験結果)が持つエントロピーは1ビットです。
これは、合否を伝えるために、理論上は「0か1か」のどちらか一方を送るだけで十分、つまり1ビットあれば事足りることを意味します。
🧠 21ビットの冗長性:「サクラサク」の驚くべき非効率
しかし、実際に使われた「サクラサク」(サクラサク)というカタカナ5文字の電報文は、当時の和文モールス符号に直すと、およそ21ビットもの情報量が必要となります。
シャノンの情報源符号化定理は、「エントロピーが1ビットの情報は1ビットで送れる」ことを保証しています。この定理に照らし合わせると、本来1ビットで済むはずの情報に21ビットも使っている「サクラサク」は、極めて冗長で非効率的だと断言できます。
「『サクラサク』はシャノン先生ブチギレ符号化」
「不合格の効率が悪すぎる長いぞ」
「エントロピーが1ビットですから。2ビットもあれば伝えられるわけですよ」
この極端な非効率性は、情報理論の父シャノンから見れば「情報源不合格定理のこと知らんの?って言いたくなりますよね」というレベルの符号化でした。
[補足:21ビットの根拠]
和文モールス符号のカタカナ一文字あたりの平均符号長は約4.2ビットとされ、5文字で送る「サクラサク」は、4.2ビット × 5文字 ≒ 21ビットとなり、わずか1ビットの情報伝達に極めて非効率な冗長性を持たせていたことがわかります。
ここがポイント👌
受験結果(合否)という情報源のエントロピーは1ビットですが、「サクラサク」の電報は和文モールス符号で約21ビットもの情報量を使っており、情報理論の観点から極めて非効率的な符号化である。これは、現代のデータ通信における圧縮技術(符号化)の重要性を逆説的に示しています。
⚡ モールス信号 効率の秘密:出現頻度に基づく最適な符号化設計
「サクラサク」のように冗長な符号化がある一方で、情報理論の原則に忠実に、効率を極限まで追求した符号化の事例として、モールス信号の設計が挙げられます。
モールス信号の巧妙さは、「送る人にとって一番楽」になるように最適化されている点にあります。
「モールス信号ってエライン送る人にとって一番楽なようになってるんですよ」
頻度の高い文字を短くする原則
モールス信号における工夫は、出現頻度の高い文字ほど、短い符号を割り当てるという原則です。
例えば、英語の中で最もよく使われる文字「E」の符号は、最も短い「トン」(短点1つ)です。逆に、出現頻度が非常に低い文字「Q」の符号は、「ツーツートンツー」という長いものが割り当てられています。
これは、普段使いが多い文字(情報)は短く、めったに使わない文字は長くてもよい、という、情報理論の考え方(エントロピーが低い情報源には短い符号を割り当てるべき)に忠実な、最適な符号化設計なのです。
ここがポイント👌
シャノンの情報源符号化定理は、ある情報源のエントロピーを算出し、その情報量がどれだけ圧縮可能か(通信速度の限界)を究極的に示しています。モールス信号は、この定理の原則を経験則として体現しており、現代の可逆圧縮の基礎となるハフマン符号などにも通じる考え方です。
🤯 情報理論が示す通信速度の限界:「沈黙」が最高の符号化である理由
情報源符号化定理が示唆するのは、「ベストを尽くせばここまで効率化できる」という究極的な基準です。この定理は、情報源のエントロピーと同じビット数でその情報を送れることを保証し、通信技術者に対し「これ以上は良くならない」という限界を与えています。
この考え方を突き詰めると、エントロピーが0の情報源に対しては、「沈黙」すらも最高の効率を持った符号化となり得ます。
例えば、「毎日カレーしか出ない家庭」における夕食のメニューという情報源を考えましょう。この情報源は「カレー」しか結果がないため、エントロピーは0です。シャノンの定理によれば、エントロピーが0ビットの情報源に対する最良の符号は0ビット、つまり何も送らないことです。
「沈黙が最も効率いいんですよ」
この場合、家族は「今日の夕食のメニュー」を尋ねる必要がなく、沈黙こそが最も効率の良いコミュニケーションとなるのです。これは、現代のAIによる情報選別やデータ通信の省電力化といった分野にも、その哲学が受け継がれています。
💡 まとめ:サクラサクから学ぶ情報理論の価値
合格・不合格という1ビットの情報は、電報「サクラサク」では約21ビットという極めて冗長な符号化(シャノン先生ブチギレ符号化)で伝達されていました。
シャノンの情報源符号化定理は、情報源のエントロピーと同じビット数で情報を送れる、通信速度の究極の限界を保証しています。モールス信号は、出現頻度の高い情報に短い符号を割り当てることで効率を追求しており、情報理論の原則に忠実です。
情報理論の極致では、「沈黙」こそがエントロピー0の情報に対する最も効率の良い符号(0ビット)であると定義されます。私たちが何気なく行っているデータ通信やAIによる情報選別の背後には、情報理論という精緻な数学が息づいています。この理論を知ることで、現代社会の情報がどのように流れ、圧縮され、処理されているのかを、より深く理解できるようになるでしょう。
📰 配信元情報
- 番組名: ゆるコンピュータ科学ラジオ
- タイトル: 「サクラサク」はシャノン先生ブチギレ符号化。脳はスマホに繋ぐべき【情報理論4】#12
- 配信日: 2022-03-20


コメント